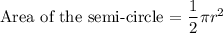Question

A square of area 32 cm2 is inscribed into a semi-circle. What is the area of the semi-circle?

Answer 1

*incorect caculations do not read*
we have a formula for that

`{r}^(2) = \frac{5 {a}^(2) }{4}`
r being the radius and a being the edge of our square

a is

`√(32)`
so lets find r

`{r}^(2) = \frac{5 * { √(32) }^(2) }{4}`
after solving we reach these two answers

`r = - 2 √(10) \\ r = 2 √(10)`
we are looking for a radius so negetive numbers are disregarded. now that we have the radius for our semi circle we can calculate the area of our semi circle. with this formula

`\frac{\pi * {r}^(2) }{2}`
(just the formula for the area of a circle divided by half)

`area = (\pi * 2√(10) )/(2) \\area = \pi * 20`

Answer 2

------------------------------------------------------------
Find Length of the square :
------------------------------------------------------------
Given that the area of the square is 32 cm²:

Area = Length²


`\text {Length =} √(32)`

------------------------------------------------------------
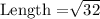
Find Radius :
------------------------------------------------------------
Using Pythagorus Theorem to find the radius of the circle:

a² + b² = c²


`( √(32))^2 + (( √(32) )/(2) )^2 = ( \text {radius} )^2`


`(\text {radius} )^2 = 32 + (32)/(4)`


`(\text {radius} )^2 = 40`


`\text { Radius = } √( 40 )`

------------------------------------------------------------
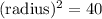
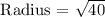
Find Area of the semi-circle :
------------------------------------------------------------

`\text {Area of the semi-circle = } (1)/(2) \pi r^2`


`\text {Area of the semi-circle = } (1)/(2) \pi ( √(40)) ^2`


`\text {Area of the semi-circle = } 20 \pi`


`\text {Area of the semi-circle = } 62.83 \ cm^2`