Answer:
The rate of the current is 5 mph.
Explanation:
Given : Kellen's boat travels 15 mph. If she can travel 2 mi upstream in the same amount of time she can go 4 mi downstream.
To find : The rate of the river current ?
Solution :
Let x be the rate of the currents .
The downstream speed is 15+x.
The upstream speed is 15-x.
We know that,
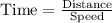
Upstream time = Downstream time
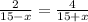
Cross multiply,
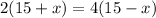
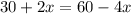
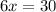
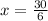
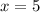
Therefore, the rate of the current is 5 mph.