Answer:
Thus, f and g are inverse functions
Explanation:
Inverse Functions
If two functions f(x) and g(x) are inverses, then it follows that:
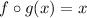
Or:
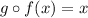
We are given
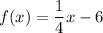
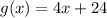
Let's test if they are inverse functions:
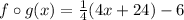
Simplifying:
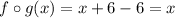
Now find:
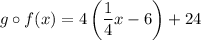
Operating:
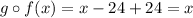
Thus, f and g are inverse functions