The triangle
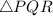 with
with
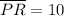 units,
units,
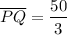 units, and area
units, and area
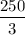 square units is one possible solution.
square units is one possible solution.
Choose the length of
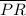
We know that the area of
 is not 6 square units, so we can choose any convenient base length that is not divisible by 6 . In this example, we will choose
is not 6 square units, so we can choose any convenient base length that is not divisible by 6 . In this example, we will choose
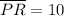 units.
units.
Calculate the height of the triangle
Since
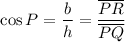 , we can solve for the height
, we can solve for the height
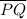 as follows:
as follows:
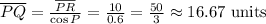
Draw the triangle
Using the Connect Line tool, draw
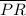 with a length of 10 units. Then, choose a point
with a length of 10 units. Then, choose a point
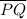 above
above
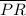 such that the height of the triangle is approximately 16.67 units. Label the points as P, Q, and R.
such that the height of the triangle is approximately 16.67 units. Label the points as P, Q, and R.
Check the area
The area of
 is calculated as:
is calculated as:
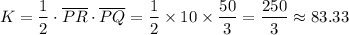 square units
square units
Since the area is not 6 square units, our triangle satisfies the given conditions.