Answer:
The correct option is : A. 7
Explanation:
According to the below diagram, for rectangle AQBC, the length
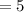 units and the width
units and the width
 units.
units.
So, the area of the rectangle
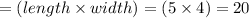 square units.
square units.
For
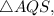 base
base
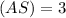 units and height
units and height
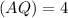 units.
units.
So, area of
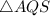
 square units.
square units.
For
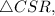 base
base
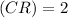 units and height
units and height
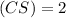 units.
units.
So, area of
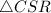
 square units.
square units.
For
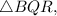 base
base
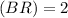 units and height
units and height
 units.
units.
So, area of
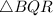
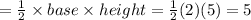 square units.
square units.
Now, total area of
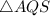 ,
,
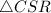 and
and
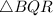
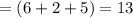 square units.
square units.
Thus, the area of
 =(Area of rectangle AQBC)-(Area of
=(Area of rectangle AQBC)-(Area of
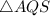 ,
,
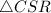 and
and
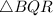 )
)
 square units.
square units.