Answer:
The mean absolute deviation of the data set is
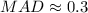
Explanation:
The mean absolute deviation of a dataset is the average distance between each data point and the mean. It gives us an idea about the variability in a dataset.
To find the mean absolute deviation you must:
1. Calculate the mean
Found by adding all data points and dividing by the number of data points.

2. Calculate how far away each data point is from the mean using positive distances. These are called absolute deviations.

3. Add those deviations together.
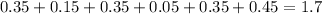
4. Divide the sum by the number of data points.
