Question

What is the horizontal asymptote of the function f(x)=(x-2)/(x-3)^2

Answer 1

The horizontal asymptote of the function is y=0.

Explanation:

Given :
`f(x)=((x-2))/((x-3)^2)`

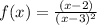
To find : What is the horizontal asymptote of the function?

Solution :

In a rational function,

If the degree of the numerator < degree of denominator then a horizontal asymptote can be found.

In the given function,

`f(x)=((x-2))/((x-3)^2)`

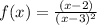
The degree of numerator is 1.

The degree of denominator is 2

The degree of the numerator < degree of denominator

When this condition satisfy then horizontal asymptote is always y=0

Therefore, The horizontal asymptote of the function is y=0.

Answer 2

To find this, take the limit of the given function as x increases without bound.  Because the highest x power in the numerator (1) is smaller than that in the denominator, f(x) tends to zero as x increases without bound.  Thus, the equation of the horiz. asy. here is y = 0.