Question

Please Help!!!!!!!!!

Answer 1

Take one triangle. Each triangle is isosceles, so if we bisect the angle at the vertex (on the center of the circle), then we end up with two right triangles. Take one of these right triangles. Its hypotenuse corresponds to the radius of the circle.

Now, if you have
`n` of those isosceles triangles, you know that the central angle of each one (angle of each vertex) is exactly
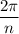
`\frac{2\pi}n` radians. This means the bisected angle has measure
`\frac\pi n`. So we can find the length of the smaller leg
`\frac b2` (
`b` because it refers to the "base" of the isosceles triangle) of each right triangle via the law of sines:


`(\sin\frac\pi n)/(\frac b2)=\frac{\sin\frac\pi2}r`

`\implies\frac b2=r\sin\frac\pi n`

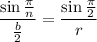
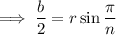
The height
`h` of each right triangle is obtained via the Pythagorean theorem:


`r^2=h^2+\left(\frac b2\right)^2=h^2+r^2\sin^2\frac\pi n`

`h^2=r^2\left(1-\sin^2\frac\pi n\right)`

`\implies h=r√(1-\sin^2\frac\pi n)`

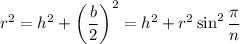
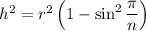
The area of each right triangle is
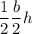
`\frac12\frac b2h`, so the area of each isosceles triangle section is
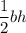
`\frac12bh`. We have
`n` triangles, so the total area that approximates the area of the circle is
`\frac n2bh`.


`\frac n2\left(2r\sin\frac\pi n\right)\left(r√(1-\sin^2\frac\pi n)\right)=nr^2\sin\frac\pi n√(1-\sin^2\frac\pi n)`

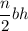
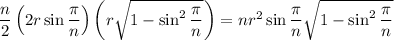
As
`n` gets arbitrarily larger, we expect the total area of the triangles to get closer to
`\pi r^2`. (With respect to the bottom graphic, we can arrange the isosceles triangles as a parallelogram, whose area would would be the product of its base and height.) We can take a limit to verify this.