Question

The graph of an equation is shown below:

line joining ordered pairs negative 3, negative 2 and 1, 3

Based on the graph, which of the following represents a solution to the equation?

(−2, −3)
(3, 1)
(1, 3)
(3, 2)

Answer 1

The point
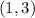`(1,3)` is a solution of the linear equation

Explanation:

we have

`A(-3,-2)\ B(1,3)`

Find the equation of the line AB

The slope of the line is equal to

`m=(y2-y1)/(x2-x1)`

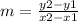
substitute the values

`m=(3+2)/(1+3)`

`m=(5)/(4)`

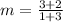
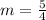
Find the equation of the into point-slope form

`y-y1=m(x-x1)`

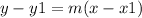
we have

`m=(5)/(4)`

`(x1,y1)=B(1,3)`

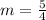
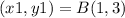
substitute

`y-3=(5)/(4)(x-1)`

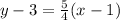
we know that

If a point is a solution to the equation of the line

then

the point must be satisfy the equation and based on the graph the point must be on the line

Let's check every point.

case A) point
`(-2,-3)`

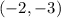
Substitute the value of x and y in the equation of the line

`-3-3=(5)/(4)(-2-1)`

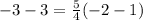
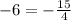`-6=-(15)/(4)` -------> is not true

The point
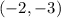`(-2,-3)` is not a solution of the linear equation

See the attached figure-------> the point is not on the line

case B) point
`(3,1)`

Substitute the value of x and y in the equation of the line

`1-3=(5)/(4)(3-1)`

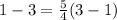
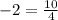`-2=(10)/(4)` -------> is not true

The point
`(3,1)` is not a solution of the linear equation

See the attached figure-------> the point is not on the line

case C) point
`(1,3)`

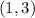
Substitute the value of x and y in the equation of the line

`3-3=(5)/(4)(1-1)`

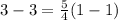
`0=0` -------> is true

The point
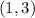`(1,3)` is a solution of the linear equation

See the attached figure-------> the point is on the line

case D) point
`(3,2)`

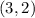
Substitute the value of x and y in the equation of the line

`2-3=(5)/(4)(3-1)`

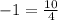`-1=(10)/(4)` -------> is not true

The point
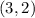`(3,2)` is not a solution of the linear equation

See the attached figure-------> the point is not on the line