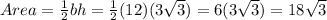Answer:
Look below
Explanation:
Given that CDB is 90 degrees, ACB is 90 degrees, and ACD is 60 degrees, we can determine that DCB = 90-60 = 30 degrees.
This means triangle BCD is a 30-60-90 (angle measures) right triangle
The proportions of the sides (from smallest to largest) is
x:x√3:2x
We are given that BC = 6 cm. This means...
2x=6
x=3
This means DB is 3 cm and CD is 3√3 cm
Using the linear pair theorem, we can find that Angle CDA is 90 degrees. This means ACD is also a 30-60-90 triangle.
x=3√3
x√3=9
2x=6√3
Now we need to find AB
AB = AD + DB
AB = 9 + 3
AB = 12 cm