Answer:
The graph of f(x) shifts 5 units right and 9 units down to graph g(x).
Explanation:
The general form of the parabola is
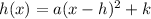
Where, (h,k) is the vertex of the parabola and a is stretch factor.
The parent function is

The vertex of the parabola is (0,0).
The given function is
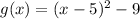
The vertex of the parabola is (5,-9).
The vertex of the parabola shifts from (0,0) to (5,-9), therefore the graph of f(x) shifts 5 units right and 9 units down to graph g(x).