Answer:
f(x) = 3x + 5 with {8, 11},
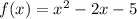 with {-6, -5},
with {-6, -5},
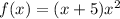 with {6, 28} and f(x) = 4-x with {3, 2}.
with {6, 28} and f(x) = 4-x with {3, 2}.
Explanation:
The domain are the possible x-values and the range are the y-values obtained with the domain. Then, let's calculate the range of each function with the given domain.
f(x) = 3x+5:
f(1) = 3(1)+5 = 3+5 = 8.
f(2) = 3(2)+5 = 6+5 = 11.
Then, the range of f(x) = 3x+5 is {8, 11}.
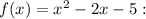
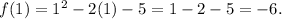
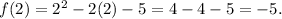
Then, the range of
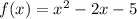 is {-6, -5}.
is {-6, -5}.
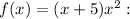
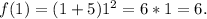
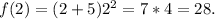
Then, the range of
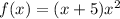 is {6, 28}.
is {6, 28}.
f(x) = 4-x:
f(1) = 4-1=3.
f(2) = 4-2 = 2.
Then, the range od f(x) = 4-x is {3,2}.