Question

Let v = (-2,6) and w = (12,4). Which of the following is true?

A. v and w are perpendicular.
B. The x-component of v is 6.
C. VxW= 48
D. w = -4(-3,-1)

Answer 1

A is the correct answer because the dot product of v and w is (-2•12)+(4•6), which in turn is equivalent to -24+24, or 0.

Answer 2

Answer: The correct option are

(A) v and w are perpendicular.

(D) w = -4(-3,-1).

Step-by-step explanation: We are given two vectors 'v' and 'w' as follows:

`v=(-2,6),\\\\w=(12,4).`

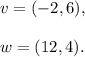
We are to select the correct statement about these two vectors.

We know that two vectors are perpendicular to each other if their dot product is zero.

We have

`v.w=(-2,6).(12,4)=-2* 12+6* 4=-24+24=0.`

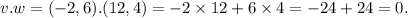
So, the two vectors are perpendicular.

Option (A) is correct.

Since the x-component of 'v' is -2, so option (B) is incorrect.

Since the product f 'v' and 'w' is 0, so it cannot equal to 48. Option (C) is also incorrect.

Now,

`w=(12,4)=-4(-3,-1).`

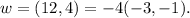
So, option (D) is also correct.

Thus, the correct options are (A) and (D).