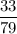Question

Out of 350 applicants for a job, 158 are female and 66 are female and have a graduate degree. step 1. what is the probability that a randomly chosen applicant has a graduate degree, given that they are female?

Answer 1

Total applicants = 350

Total female that have a degree = 66

Probability = 66/350 = 33/175

--------------------------------------------------------------------------------------------
Answer: The probability of choose a female with a degree is 33/175.
--------------------------------------------------------------------------------------------

Answer 2

Answer:
`(33)/(79)`

Explanation:

Let F= Applicants are Females.

G= Applicants have a graduate degree.

Given : Total applicants N= 350

Total applicants are females n(F)= 158

Number of applicants are females and have a graduate degree. n(F∩G)=66

Now, Probability that an applicant is female =
`P(F)=(n(F))/(N)=(158)/(350)`

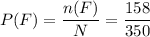
Probability that an applicant is female and have a graduate degree:

`P(F\cap G)=(n(F\cap G))/(N)\\\\=(66)/(350)`

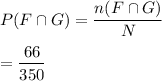
Then, the probability that a randomly chosen applicant has a graduate degree, given that they are female :-

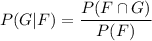`P(G|F)=(P(F\cap G))/(P(F))` [By conditional probability formula.]

`P(G|F)=((66)/(350))/((158)/(350))\\\\=(66)/(158)\\\\=(33)/(79)`

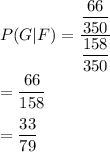
Hence, the required answer =
`(33)/(79)`