The first thing we are going to to is checking if the sequence is arithmetic of geometric. A sequence is arithmetic if it has a common difference,
. A sequence is geometric if it has a common ratio,
.
Lets test for a common difference first. To do that we are going to subtract the current term from the previous term:
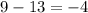
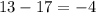
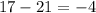
Since we have a common difference,
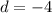
, or sequence is arithmetic.
Now, to find its 105 term, we are going to find its explicit formula using the general form of an arithmetic sequence:
where
is the nth term
is the first term
is the position of the term in the sequence
is the common diference
We can infer for our sequence that
, and for previews calculations we know that
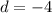
. So lets replace those values:
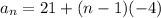
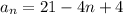
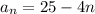
Finally, to find the 105th term of the sequence, we just need to replace
with 105 in our explicit formula:
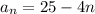
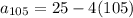
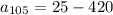
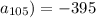We can conclude that the 105th term of the sequence is -395.