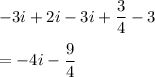Question

Write -3i+(3/4+2i)-(9/3+3i) as a complex number in standard form.

Answer 1

-3i+3/4+2i-9/3-3i=(3/4-9/3) +(-3i+2i-3i)=(3/4-3)+(-4i)=(3/4-12/4)-4i=
=-9/4-4i

Answer 2

The complex number in standard form is given by:

`-4i-(9)/(4)`

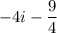
Explanation:

The expression in terms of the complex number is given by:

`-3i+((3)/(4)+2i)-((9)/(3)+3i)`

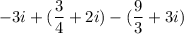
which is given by:

`-3i+((3)/(4)+2i)-(3+3i)`

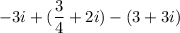
Now on opening the parentheses term we have:

`-3i+(3)/(4)+2i-3-3i`

( since, if the sign before the parentheses term is negative then the sign of each of the terms inside parentheses get's interchanged )

Now, on combining the like terms we have:

`-3i+2i-3i+(3)/(4)-3\\\\=-4i-(9)/(4)`