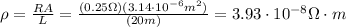The relationship between resistance R and resistivity
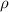
is
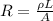
(1)
where L is the length of the wire and A is the cross-sectional area.
In our problem, the radius of the wire is half the diameter: r=1 mm=0.001 m, so the cross-sectional area is
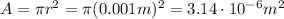
The length of the wire is L=20 m and the resistance is
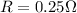
.
By re-arranging equation (1), we can find the resistivity of the wire: