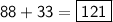This is actually formed by a triangle and a rectangle.
We can split the figure from Point C up. This would leave us with a rectangle of length 11 and width 8 and a triangle with height 11 and base 6. Use the formulas of the area of a rectangle and triangle to find the areas:
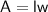
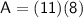
Multiply:
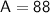
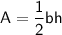
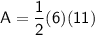
Multiply:
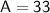
Add the two areas together to find the total area: