Question

A factory worker pushes a 30.0-kg crate a distance of 4.5 m along a level floor at constant velocity by pushing horizontally on it. the coefficient of kinetic friction between the crate and the floor is 0.25. (a) what magnitude of force must the worker apply

Answer 1

The crate moves at constant velocity, this means that its acceleration is zero, so the net force acting on the crate is zero (Newton's second law).

There are only two forces acting on the crate: the force F applied by the worker and the frictional force, acting in the opposite direction:
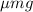
`\mu m g`, where
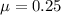
`\mu=0.25` is the coefficient of friction and
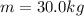
`m=30.0 kg` is the mass of the crate. Since the net force should be equal to zero, the two forces must have same magnitude, so we have:

`F=\mu m g=(0.25)(30.0 kg)(9.81 m/s^2)=73.8 N`
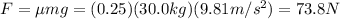
And so, this is the force that the worker must apply to the crate.