Question

Iced tea, x, costs $4 per gallon and lemonade, y, costs $6 per gallon. You need to purchase at least 9 gallons of drinks for a neighborhood picnic, but have at most $55 to spend. Model the scenario with a system of inequalities. Which of the following options represents a possible solution to the system of inequalities?

A. (10,10)
B. (10, -5)
C. (2,10)
D. (10,1)

Answer 1

4x + 6y =< 55 (because $4 per gallon of iced tea $6 per gallon of lemonade and $55 to spend)
x+y => 9

only one that works out if you test them is D. 10 * 4 is 40 1 * 6 is 6 40 + 6 is 46 46 is less than 55

Answer 2

The possible solution to the system of inequalities is:

Option: D

D. (10,1)

Explanation:

Iced tea, x, costs $4 per gallon and lemonade, y, costs $6 per gallon.

You need to purchase at least 9 gallons of drinks for a neighborhood picnic, but have at most $55 to spend.

This means that the inequalities that will be formed using the above information is:

`x+y\geq 9----------(1)`

and
`4x+6y\leq 55----------(2)`

Now, we will put the point in the given two inequalities and check which point holds true.

A)

(10,10)

Putting this point in the second inequality we have:

`4* 10+6* 10\leq 55\\\\i.e.\\\\40+60\leq 55\\\\i.e.\\\\100\leq 55`

which is not true.

Hence, Option: A is incorrect.

B)

(10,-5)

Putting this point in first inequality we have:

`10-5\geq 9\\\\i.e.\\\\5\geq 9`

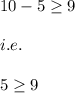
which is not true.

Hence, option: B is not true.

C)

(2,10)

Putting this point in second inequality we have:

`4* 2+6* 10\leq 55\\\\i.e.\\\\8+60\leq 55\\\\i.e.\\\\68\leq 55`

which is not true.

Hence, Option: C is incorrect.

D)

(10,1)

Putting this point in first inequality we have:

`10+1\geq 9\\\\i.e.\\\\11\geq 9`

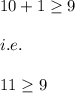
which is true.

Putting this point in second inequality we have:

`4* 10+6* 1\leq 55\\\\i.e.\\\\40+6\leq 55\\\\i.e.\\\\46\leq 55`

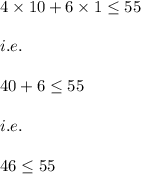
which is again true.

Hence, (10,1) is a possible solution to the system of inequalities.