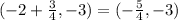We have to find the focus of the parabola with equation:
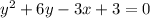
In order to find the focus, we first need to convert the equation of parabola to its standard form, as shown below:
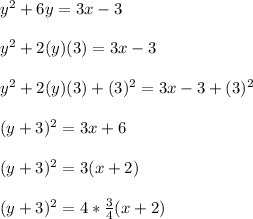
Comparing this equation to the similar general equation of parabola, we get:
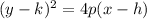
k = -3
p= 3/4
h = - 2
The focus of the general parabola is located at ( h+p, k)
Using the values, we get:
Focus of the given parabolic satellite =