Question

Find an equation in standard form for the hyperbola with vertices at (0, ±10) and asymptotes at y = ±five divided by four times x..

Answer 1

so, based on the provided vertices, the hyperbola will look more or less like the picture below, with those asymptotes, so is a vertical hyperbola.

since the center is at the origina, that makes the traverse axis of 20, namely a = 10, what is "b" then?


`\bf \textit{hyperbolas, vertical traverse axis } \\\\ \cfrac{(y- k)^2}{ a^2}-\cfrac{(x- h)^2}{ b^2}=1 \qquad \begin{cases} center\ ( h, k)\\ vertices\ ( h, k\pm a)\\ c=\textit{distance from}\\ \qquad \textit{center to foci}\\ \qquad √( a ^2 + b ^2)\\ asymptotes\quad y= k\pm \cfrac{a}{b}(x- h) \end{cases}\\\\ -------------------------------`


`\bf \pm\cfrac{5}{4}x~~=~~k\pm \cfrac{a}{b}(x- h)\implies \pm\cfrac{5}{4}x~~=~~0\pm \cfrac{a}{b}(x- 0) \\\\\\ \pm\cfrac{5}{4}x~~=~~\pm\cfrac{a}{b}x\impliedby \begin{array}{llll} \textit{let us use the positive one}\\ \textit{and since we know }a=10 \end{array} \\\\\\ \cfrac{5x}{4}=\cfrac{10x}{b}\implies \cfrac{5x}{10x}=\cfrac{4}{b}\implies \cfrac{1}{2}=\cfrac{4}{b}\implies b=8\\\\ -------------------------------\\\\ \cfrac{(y-0)^2}{10^2}-\cfrac{(x-0)^2}{8^2}=1\implies \cfrac{y^2}{100}-\cfrac{x^2}{64}=1`

Answer 2

The equation of hyperbola is
`(y^2)/(10^2)-(x^2)/(8^2)=1`.

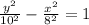Explanation:

Given information: Vertices at (0, ±10) asymptotes at
`y=\pm (5)/(4)x`.

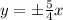Vertices are on the y-axis, so given hyperbola is along the y-axis. The standard form for the hyperbola is

`((y-k)^2)/(b^2)-((x-h)^2)/(a^2)=1`

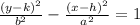
where, (h,k) is the center of hyperbola. (0,±b) are vertex and
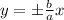`y=\pm (b)/(a)x` are asymptotes.

Vertices at (0, ±10), it means center of the hyperbola is (0,0). So the standard form for the hyperbola is

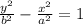`(y^2)/(b^2)-(x^2)/(a^2)=1` .... (1)

Vertices of hyperbola:

`(0,\pm b)=(0, \pm 10)`

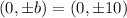
On comparing we get

`b=10`

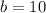
The value of b is 10.

Asymptotes of the hyperbola:

`\pm (b)/(a)x=\pm (5)/(4)x`

On comparing both sides, we get

`(b)/(a)=(5)/(4)`

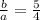
Substitute b=10.

`(10)/(a)=(5)/(4)`

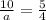
On cross multiplication,

`40=5a`

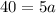
Divide both sides by 5.

`8=a`

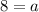
The value of a is 8.

Substitute a=8 and b=10 in equation (1) to find the equation of hyperbola.

`(y^2)/(10^2)-(x^2)/(8^2)=1`

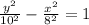
Therefore the equation of hyperbola is
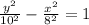`(y^2)/(10^2)-(x^2)/(8^2)=1`.