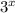Answer:
The equivalent expressions are:
C.
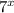
D.
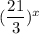
E.
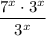
Explanation:
We are asked to find the algebraic expression that is equivalent to the expression:
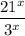
A)

We know that this expression is incorrect.
Since,
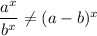
B)
7
This option is also incorrect.
Since,
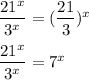
C)
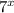
This option is true.
Since,
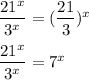
D)
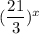
This option is true.
Since,
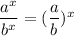
E)
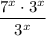
This option is correct.
Since,

F)
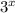
This option is incorrect.
Since we get a expression as:
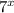 but not
but not