Answer:

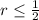 .
.
Step-by-step explanation:
Given,
the inequality

By dividing 6 on both sides then we get
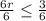
By simplication we get the inequality
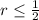
It means values of r can be any value less than
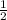 .
.
Therefore , we get maximum value of
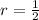
Therefore, the values of r can be from negative infinity to
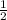 .
.
Therefore , the set of values of r can be write as
![\left\{-\infty,(1)/(2) \right ]](https://img.qammunity.org/2019/formulas/mathematics/college/qkw2uyfl038gas664d276edpnf2paro69i.png) .
.