Answer:
7 sq.units.
Explanation:
Q=(6, -2)
R=(4, -7)
S=(2, -5)
Now find the sides of triangle QR,RS,QS
To find QR use distance formula :

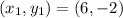
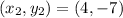
Substitute the values in the formula :
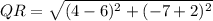

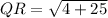
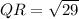
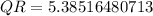
To Find RS
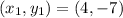
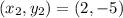
Substitute the values in the formula :

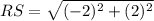

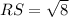
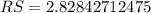
To Find QS
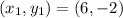
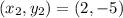
Substitute the values in the formula :
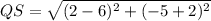
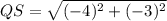
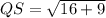
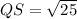
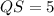
So, sides of triangle :
a =5.38516480713
b=2.82842712475
c=5
Now to find area:
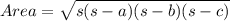
Where
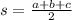
a,b,c are the side lengths of triangle
Now substitute the values :
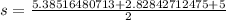
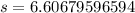
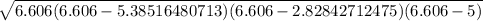
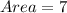
Hence the area of the given triangle is 7 sq. units.