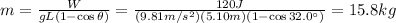Question

You do 120 j of work while pulling your sister back on a swing, whose chain is 5.10 m long. you start with the swing hanging vertically and pull it until the chain makes an angle of 32.0° with the vertical with your sister is at rest. what is your sister's mass, assuming negligible friction?

Answer 1

The work done to pull the sister back on the swing is equal to the increase in potential energy of the sister:

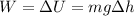
`W= \Delta U = mg \Delta h` (1)

where m is the sister's mass, g is the gravitational acceleration and
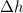
`\Delta h` is the increase in altitude of the sister with respect to its initial position.

By calling
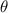
`\theta` the angle of the chain with respect to the vertical, the increase in altitude is given by

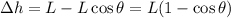
`\Delta h = L - L \cos \theta = L(1 - \cos \theta)` (2)
where L is the length of the chain.

Putting (2) inside (1), we find

`W= m g L (1 - \cos \theta)`
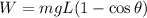
from which we can find the mass of the sister:

`m = (W)/(g L (1 - \cos \theta)) = (120 J)/((9.81 m/s^2)(5.10 m)(1- \cos 32.0^(\circ))) =15.8 kg`