Question

Solve the triangle. Round the side lengths to the nearest tenth of a centimeter.​

Answer 1

Check the picture below.

we know the angles at the "base" are 70° each, so we have twin angles and thus we'd also have twin sides stemming from the "vertex" as you see in the picture, that means if we were to run an angle bisector from the "vertex" down to the "base", the line will be perpendicular to the "base" as you see there, so we can simply use SOH CAH TOA to get the side "s", or namely the cosine.

`cos(70^o)=\cfrac{\stackrel{adjacent}{5}}{\underset{hypotenuse}{s}}\implies s=\cfrac{5}{cos(70^o)}\implies s\approx 14.6`

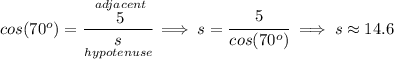
and if you wonder what the "vertex" angle is, well simply 180° - 70° - 70° = 40°.