The given data are:
E = 2% = 0.02
z = 1.96
p = 72% = 0.72
Start from the margin of error formula:
E = z
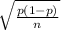
And solve for n = sample size
n = (z/E)² · p · (1-p)
= (1.96 / 0.02)² · 0.76 · (1 - 0.76)
= 1751.7696
You need to round up to the nearest integer (because you cannot survey half of a person...); the correct answer is:
you need to survey 1752 housholds.