Question

A 10,000 kg spaceship decelerates uniformly to reduce its speed from 3,500 km/h to 1,700 km/hr in 1 s. what net force acted on this spaceship

Answer 1

First, let's calculate the initial and final speed of the spaceship:

`v_i = 3500 km/h = 972.2 m/s`

`v_f = 1700 km/h = 472.2 m/s`

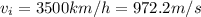
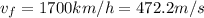
By using the initial and final speed, we can calculate the acceleration of the spaceship:

`a= (v_f-v_i)/(t)= (472.2 m/s-972.2 m/s)/(1 s)= -500 m/s^2`
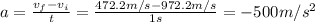
where the negative sign means it is directed against the motion of the spaceship (in fact, the spaceship is decelerating).

And now, by using Newton's second law:

`F=ma`
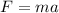
we can calculate the net force that acted on the spaceship:

`F=(10000 kg)(-500 m/s^2)=-5 \cdot 10^6 N`
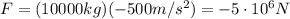
where the negative sign means it is directed against the direction of motion of the spaceship.