Question

Can someone help me with this whole back page ?

Answer 1

for 1a,
set x=0 to find y-intercept.
set y=0 to find x-intercept.

the function is a positive parabola and is shown in the first image.

for 1b,
same process, similar looking graph shown in the second image.

for 2,

`area = 4\pi {r}^(2) = 196\pi \: {in}^(2)`


`{r}^(2) = 49 \: {in}^(2)`


`r = 7 \: in`

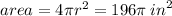
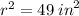
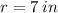
for 3, (refer to third image)
we'll use Pythagorean theorem


`{a}^(2) + {b}^(2) = {c}^(2)`

`{x}^(2) + {(2x)}^(2) = {h}^(2)`

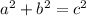
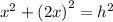
simplify and put it into a standard form:


`5{x}^(2) = 45`

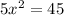
quadratic equation:


`{x}^(2) - 9 = 0`

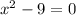
then solve for x:


`x = √(9) = 3cm`

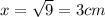
so one leg is 3cm
the other is two times that (6cm)