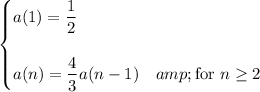Question

Hi, I'm actually a good student i do my own work but this stuff makes no sense to me, my teacher isn't the best so if you could provide a answer and IF possible a explanation for each problem on how you got it, it would be great. also kind of needed asap. thank you.

1. enter the explicit rule for the geometric sequence
15,3,3/5,3/25,...

an= _

2. enter a recursive rule for the geometric sequence
10,-80,640,-5120,...

a1=_; an=_

3. the reursive rule for the a geometric sequence is given
a1= 2; an= 1/3 an-1

enter the explicit rule for the sequence

an=_

4. the explicit rule for the sequence is given
an= 1/2(4/3)n-1

enter the recursive rule for the geometric sequence
a1=_; an=_

Answer 1

1. Starting with 15, each successive term is obtained by multiplying by
`\frac15`. So the explicit rule for the sequence must be


`a(n)=15\left(\frac15\right)^(n-1)`

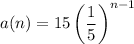
2. Starting with 10, the next terms are obtained by multiplying by -8. So the recursive rule would be


`\begin{cases}a(1)=10\\a(n)=-8a(n-1)&\text{for }n\ge2\end{cases}`

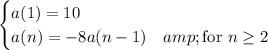
3. We're given the recursive rule,


`\begin{cases}a(1)=2\\a(n)=\frac13a(n-1)&\text{for }n\ge2\end{cases}`

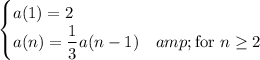
We have


`a(n)=\frac13a(n-1)=\left(\frac13\right)^2a(n-2)=\left(\frac13\right)^3a(n-3)=\cdots=\left(\frac13\right)^(n-1)a(1)`

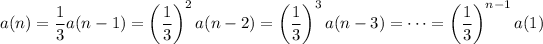
so the explicit rule is


`a(n)=2\left(\frac13\right)^(n-1)`

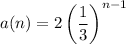
4. We're given the explicit rule


`a(n)=\frac12\left(\frac43\right)^(n-1)`

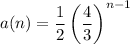
When
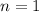
`n=1`, we get the first term to be
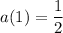
`a(1)=\frac12`. For each successive term, we have to multiply by
`\frac43`. So the recursive rule is


`\begin{cases}a(1)=\frac12\\\\a(n)=\frac43a(n-1)&\text{for }n\ge2\end{cases}`