Question

A. Use composition to prove whether or not the functions are inverses of each other.

B.Express the domain of the compositions using interval notation
f(x)= 1/x-5, g(x)=5x+1/x

Answer 1

They switched the 1/x to a positive and the added 5x. The domains are 1, 2, 3, 4, -5, -4, -3, -2, -1, 0. Hope this helps. 

Answer 2

Answer with explanation:

If f(x) and g(x) are two functions which are Inverses of each other then

either of two will be true.

→fog(x)=x

→ gof (x)=x

⇒fog(x)

=f[g(x)]

`=f((5 x+1)/(x))\\\\=f({5+(1)/(x)})\\\\=\frac{1}{({5+(1)/(x)-5})}\\\\=(1)/((1)/(x))\\\\=x`

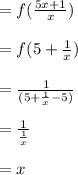
→ gof (x)

=g[f(x)]

`=g((1)/(x-5))\\\\=5+(1)/((1)/(x-5))\\\\=5+x-5\\\\=x`

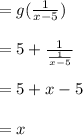
Which shows that f(x) and g(x) are inverses of each other.

→Domain of f(x)= All Real numbers excluding 5=R-{5}

→Domain of g(x)=All Real numbers excluding 0=R-{0}

→Domain of fog(x)=All Real numbers