Answer:
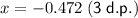
Explanation:
Given equation:
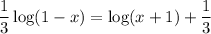

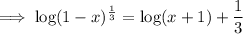
Subtract log(x + 1) from both sides:
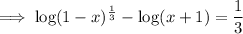
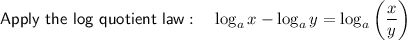
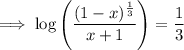
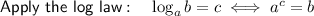
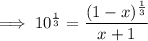
![\textsf{Apply the exponent rule}: \quad a^{(1)/(n)}=\sqrt[n]{a}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/vr1wh8xpa2l9wian0tq5.png)
![\implies \sqrt[3]{10} =\frac{\sqrt[3]{1-x}}{x+1}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/5nunzogxvzib3iv2558p.png)
Multiply both sides by (x + 1):
![\implies \sqrt[3]{10}(x+1)=\sqrt[3]{1-x}}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/zo6wi0jcsvac1afic16d.png)
Cube both sides:
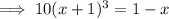
Expand the left side:

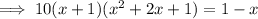


Subtract 1 and add x to both sides:

Find the roots of the cubic function by graphing, using a calculator, or by a numerical method.
Real root:
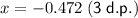
Complex roots:
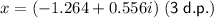

Therefore, the only valid solution is the real root:
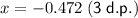
As we can only take logs of positive numbers, substitute the real root into (1 - x) and (x + 1) to check:
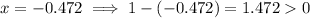
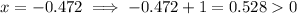
As both results are positive, this is a valid solution for the given equation.
(Proof of the solution is in the attached graph).