Question

Given the function f(x)= x2-81/x2-11x+18 on your graphing calculator, what is the most appropriate viewing window to see the graph?

a Xmin: –10, Xmax: 10
Ymin: –10, Ymax: 10

b Xmin: –5, Xmax: 5
Ymin: –5, Ymax: 5

c Xmin: 0, Xmax: 10
Ymin: 0, Ymax: 10

d Xmin: –10, Xmax: 0
Ymin: –10, Ymax: 0

i figured it out, its a

Answer 1

i think is A not sure

Answer 2

The correct option is a.

Explanation:

The given function is

`f\left(x\right)=(\left x^2-81\right)/(x^2-11x+18)`

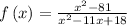
It can be written as

`f\left(x\right)=(\left(x-9)(x+9))/((x-9)(x-2))`

`f\left(x\right)=(\left x+9)/(x-2)`

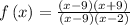
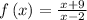
Put x=0 to find y-intercept.

`f(0)=(0+9)/(0-2)=-4.5`

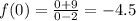
The y-intercept is (0,-4.5).

Put f(x)=0 to find x-intercept.

`0=(x+9)/(x-2)\Rightarrow x=-9`

The x-intercept is (-9,0).

Equate denominator equal to 0, to find the vertical asymptote.

`x-2=0\Rightarrow x=2`

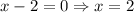
The vertical asymptote is x=2.

Take limit x tends to infinity, to find horizontal asymptote.

`lim_(x\rightarrow \infty)f(x)=lim_(x\rightarrow \infty)(x+9)/(x-2)`

`lim_(x\rightarrow \infty)f(x)=lim_(x\rightarrow \infty)(x(1+(9)/(x)))/(x(1-(2)/(x)))`

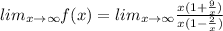
Apply limits,

`lim_(x\rightarrow \infty)f(x)=1`

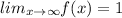
The horizontal asymptote is y=1.

Since the intercepts and asymtotes lie in the window, i.e., Xmin: –10, Xmax: 10

, Ymin: –10, Ymax: 10, thus the correct answer would be option a.