Answer: There are maximum 8 points that lie in Quadrant 2.
Explanation:
Since the graph f(x) consists of 14 points.
Number of points lie in Quadrant 1 of the coordinate plane = 6
Since f(x) is an odd function.
So, it has rotational symmetry with respect to origin i.e. the graph remains unchanged after rotation of 180 degrees about the origin.
Hence, the greatest number of points that can lie in Quadrant 2 is given by
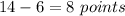
Hence, there are maximum 8 points that lie in Quadrant 2.