We can write the unknown number as
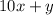
, where both
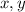
are in the set

. (Neither can be 0)
Interchanging the digits makes the number
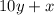
. So
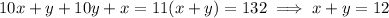
Adding 12 to the number makes it 5 times the sum of the number's digits, which means
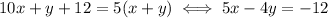
Now we can solve the system,
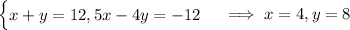
so the original number is 48.