Question

The half life of cobalt-60 is 5.27 years, approximately how much of a 199 g sample will remain after 20 years

Answer 1

Radioactive decay is expressed by the following formula:

`N_(t) = N_(0) e^(-lambda * t)`
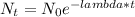
N₀ is the initial number of undecayed atoms.
Nt is the number of undecayed atoms remaining after time t
λ is the decay constant.
The relationship between λ and the half life time t1/2 is:
λ =
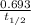
`(0.693)/( t_(1/2) )` = 0.693 / 5.27 = 0.1315
`y^(-1)`
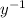
Taking natural logs for both sides of the decay expression:
ln Nt = ln N₀ - λ t
ln Nt = ln 199 - (0.1315 x 20)
= 5.293 - 2.63 = 2.66
From which:
Nt = 14.29 g