Answer: 0.121
Explanation:
Given : The manufacturer of a new compact car claims the miles per gallon (mpg) for the gasoline consumption is mound-shaped and symmetric i.e. a normal distribution with
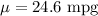
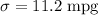
Sample size : n= 30
Let x be a random variable that represents the gasoline consumption.
Z-score :
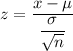
For x= 27
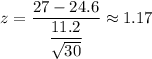
Now, the probability the average mpg achieved by these 30 cars will be greater than 27 will be :-
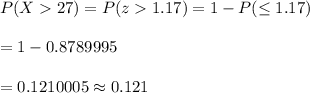
Hence, the probability the average mpg achieved by these 30 cars will be greater than 27 = 0.121