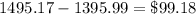Answer:
The difference between the monthly payments is
Explanation:
We know that,
![\text{PV of annuity}=P\left[(1-(1+r)^(-n))/(r)\right]](https://img.qammunity.org/2019/formulas/business/high-school/zcse4794vfy1xax0rqcm9afqw3lklci9bi.png)
Where,
PV = Present value of annuity,
P = payment per period,
r = rate of interest per period,
n = number of period.
Monthly payment for 25 years.
![\Rightarrow 165000=P\left[(1-(1+(0.091)/(12))^(-25* 12))/((0.091)/(12))\right]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/pz98viqwehloqnl0npkggctmuae5xyanvk.png)
![\Rightarrow P=(165000)/(\left[(1-(1+(0.091)/(12))^(-300))/((0.091)/(12))\right])=\$1395.99](https://img.qammunity.org/2019/formulas/mathematics/middle-school/r5o410tw5xk1azjr5ifzw6ile8w9npjkyo.png)
Monthly payment for 20 years.
![\Rightarrow 165000=P\left[(1-(1+(0.091)/(12))^(-20* 12))/((0.091)/(12))\right]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/4zk7p72lvxg24hp46xhd3bu2n0ns1cv0cq.png)
![\Rightarrow P=(165000)/(\left[(1-(1+(0.091)/(12))^(-240))/((0.091)/(12))\right])=\$1495.17](https://img.qammunity.org/2019/formulas/mathematics/middle-school/koqpob3o3xaotgcm2mm50x1x0fgpuh57by.png)
Therefore, the difference between the monthly payments is