Answer:
The general value of x is
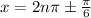 , where n is any integer. The values of x between 0 to 2π are
, where n is any integer. The values of x between 0 to 2π are
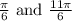 .
.
Explanation:
It is given that
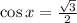
We know that
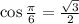
So, the given equation can be written as
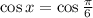
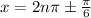
Where, n is any integer.
For n=0,

For n=1,
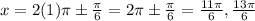
Therefore the general value of x is
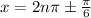 , where n is any integer. The values of x between 0 to 2π are
, where n is any integer. The values of x between 0 to 2π are
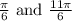 .
.