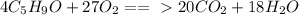Question

Balance the reaction: C5H90 + 02 = C02 + H20

Answer 1

Start by balancing the hydrogen atoms. There are 9 on the reactants side and 2 on the products side. The least common multiple of 9 and 2 is 18, so the coefficient for C5H9O should be 2 and the coefficient for H2O should be 9.

Next, balance the carbon atoms. After giving C5H9O a coefficient of 2, there are 2*5, or 10 carbon atoms on the reactants side. There is only 1 carbon on the products side. The least common multiple of 1 and 10 is 10, so the coefficient of C5H9O remains as 2 and the coefficient for CO2 becomes 10.

Lastly, balance the oxygen atoms. With C5H9O having a coefficient of 2, there are 4 oxygen atoms on the reactants side. With CO2 having a coefficient of 10 and H2O having a coefficient of 9, there are 29 oxygen atoms on the products side. Here, you balance by changing only the coefficient of O2, which currently provides 2 oxygen atoms to the reactants side. 2 of the 29 oxygen atoms are covered by C5H9O, so the O2 needs to cover for the other 27. Every mole of O2 has 2 oxygen atoms, so the coefficient should be 27/2, or 13.5. We don't want decimals in the reaction, so multiply all of the coefficients by two. This gives the balance reaction:

4C5H9O + 27O2 --> 20CO2 + 18H2O

Answer 2

When you balance a reaction, you want the same number of atoms of each element on both sides of the arrow/in the reactants (left side) and products (right side). For example, if there are four oxygen on the left, you want four oxygen on the right and if there are three hydrogen on the left, you want three hydrogen on the right, etc.

So your equation is:

`C_(5)H_(9)O + O_(2) ==\ \textgreater \ CO_(2) + H_(2)O`

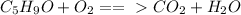
On the left, you have 5 carbon, 9 hydrogen, and 3 oxygen.
On the right, you have 1 carbon, 2 hydrogen, and 3 oxygen.

You want the same numbers of each on both sides. To do this you have to multiply the compounds by adding numbers to the front of them. You can never add subscripts. Most of the time, you are reasonably guessing and checking to see which numbers work, concentrating on one element at a time.

I balanced the H's first, since there are 9 on the left and 2 on the right. You want a number that is a multiple of both. I tried 18 at first, meaning
`C_(5)H_(9)O` had to be multiplied by 2 and
`H_(2)O` by 9. However, I ran into trouble with the O's because that meant I would end up with an even number of O's on the left, no matter what I multiplied
`O_(2)` by, and an odd number of O's on the right.

That meant I would have to use 36 as my next least common multiple of 9 and 2, giving
`C_(5)H_(9)O` a coefficient of 4 and
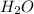
`H_(2)O` a coefficient of 18. Everything else balanced out from there. There were 20 C's on the right because of
`4C_(5)H_(9)O` (from the left). And
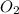
`O_(2)` had a coefficent of 27 because there were already 4 on the left, and 58 on the right, so 58-4 = 57, divided by 2 (2 oxygen atoms in
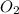
`O_(2)`) = 27.

The final equation was:

`4C_(5)H_(9)O + 27O_(2) ==\ \textgreater \ 20CO_(2) + 18H_(2)O`