Question

PLEASE!!!!!!Use the diagram and complete the steps to find the measure of the angle of depression from the top of the hoop to Lisa. The length of the shortest leg of the right triangle that is formed is __ feet. The angle of depression from the hoop to Lisa is ____ (congruent, complementary, supplementary) to the angle of elevation from Lisa’s line of sight to the hoop. Because the lengths of the opposite and adjacent sides are known, use the ___ (inverse sine, inverse cosine, inverse tangent) function. The angle of depression, rounded to the nearest degree, is approximately __(19, 21, 71) degrees.

Answer 1

The calculated angle of depression, rounded to the nearest degree, is approximately 19 degrees.

To find the measure of the angle of depression from the top of the hoop to Lisa, we need to use a bit of trigonometry. The length of the shortest leg of the right triangle that is formed is 3.5 feet. The angle of depression from the hoop to Lisa is congruent to the angle of elevation from Lisa’s line of sight to the hoop due to alternate interior angles in parallel lines.

Because the lengths of the opposite (3.5 ft) and adjacent (10 ft) sides are known, use the inverse tangent function to find the angle. This function is selected because it relates the opposite side to the adjacent side in a right triangle.

Calculating the angle of elevation (which is the same as the angle of depression), we have:

`angle = \tan^-1 ((opposite)/(adjacent))`

`angle = \tan ^-1 ((3.5)/(10)).`

This calculation will give us the angle in degrees, which rounded to the nearest degree, is approximately 19 degrees.

Answer 2

Labelled the diagram as shown below.

From the given diagram:

Vertical distance from hoop to ground (AB) = 8.5 ft

BC=ED= 10 ft

BE = 5 ft

AE = AB-BE = 8.5 - 5 = 3.5 ft

First find the length of the shortest leg of the right triangle.

In a right angle triangle AED.

ED = 10 ft

AE = 3.5 ft

Since, ED > AE

therefore, the length of the shortest leg of the right triangle that is formed is _3.5_ feet.

We know that:

The angle of depression is congruent to the angle of elevation as they form congruent angles on different parallel lines cut by a transversal line.

Therefore:

The angle of depression from the hoop to Lisa is __Congruent__ to the angle of elevation from Lisa’s line of sight to the hoop.

Use tangent ratio:

`\tan \theta = \frac{\text{Opposite side}}{\text{Adjacent side}}`

In triangle AED

Opposite side = AE = 3.5 ft

Adjacent side = ED = 10 ft

then;

`\tan \theta = (3.5)/(10) = 0.35`

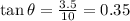
where,
`\theta` is the angle of elevation.

⇒
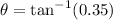`\theta = \tan^(-1) (0.35)` =19.2900462192 degree

The angle of elevation to the nearest degree is approximately, 19 degrees.

We know:

Angle of depression = Angle of elevation = 19 ft

⇒the angle of depression, rounded to the nearest degree, is approximately 19 ft.

Complete steps are shown below:

The length of the shortest leg of the right triangle that is formed is _3.5_ feet.

The angle of depression from the hoop to Lisa is __congruent__ (congruent, complementary, supplementary) to the angle of elevation from Lisa’s line of sight to the hoop.

Because the lengths of the opposite and adjacent sides are known, use the _inverse tangent_ (inverse sine, inverse cosine, inverse tangent) function. The angle of depression, rounded to the nearest degree, is approximately 19__(19, 21, 71) degrees.