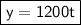Look for what 'y' is when t = 1 and t = 2. Go to the graph, look at 1 on the bottom axis and go up till you find the point, then go all the way to the left to see what the y-value is, in this case it should be 1200. If you do the same with t = 2, you will get 2400. So our two ordered pairs are:
(1, 1200), (2, 2400)
We can find the slope of these two points by plugging them into the slope formula:
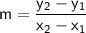
For points in the form of (x1, y1), (x2, y2). Plug in what we know:
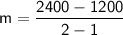
Subtract:
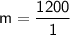
Divide:
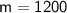
This is the slope, so we can write the equation: