Question

Silvio is an air-traffic controller who must calculate the altitude of an incoming plane. He sees the plane at an angle of elevation of 40 as it flies over a signal tower. Silvio knows the signal tower is 3 miles away, so he creates a trigonometric model to calculate the altitude of the plane relative to his own position.

Part A: Did Silvio choose the most appropriate function family for his model?
Part B: Which function family correctly models this situation?

Answer 1

Since the problem is not telling us the height of Silvio, we are going to assume it is not relevant for our calculations.
Let
`h` the altitude of the incoming plane. We know for our problem that the distance between Silvio and the tower is 3 miles, Also we know that the angle of elevation to the plane is 40°. With this information we can create a triangle as shown in the figure. We need a function that relates the angle of elevation with its opposite and adjacent sides, that function is tangent.

`tan \alpha = (opposite.side)/(adjacent.side)`

`tan(40)= (h)/(3)`

`h=3tan(40)`

`h=2.5miles`

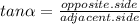
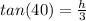
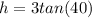
We can conclude that we should use the trig function tangent to model this situation; also, we can conclude that the equation that describes this situation is
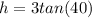
`h=3tan(40)`.