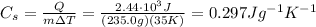Question

A 235.0 g metal block absorbs 2.44 × 103 J of heat to raise its temperature by 35 K. What is the specific heat of the metal? Show your work.

Answer 1

When an object absorbs an amount of energy equal to Q, its temperature raises by
`\Delta T` following the formula

`Q=m C_s \Delta T`
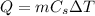
where m is the mass of the object and
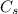
`C_s` is the specific heat capacity of the material.

In our problem, we have
`Q=2.44 \cdot 10^3 J`,
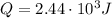
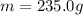
`m=235.0 g` and
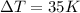
`\Delta T=35 K`, so we can re-arrange the formula and substitute the numbers to find the specific heat capacity of the metal:

`C_s = (Q)/(m \Delta T)= (2.44 \cdot 10^3 J)/((235.0 g)(35 K))=0.297 J g^(-1) K^(-1)`