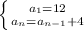Question

What is the recursive formula for this sequence? 12, 16, 20, 24, 28, ...

Answer 1

Option A is correct.

`a_1 = 12`

`a_n = a_(n-1)+4`

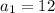
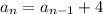
Explanation:

For a sequence
`a_1, a_2, a_3, . . . , a_n, . . .`

A recursive formula states that it is a formula that requires the computation of all previous terms in order to find the value of
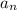`a_n` i,e it is given by;

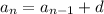`a_n = a_(n-1)+d` ......[1]

Given the sequence : 12, 16, 20, 24, 28, .......

here,

First term =
`a_1 = 12`

`a_2 = 16`

`a_3 = 20`

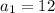
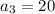
`a_4 = 24` and so on....

Now, find the common difference(d);

Common difference states that it is the difference between two numbers in an arithmetic sequence

Therefore, from the given sequence ;

d = 4

Since,

16 -12 = 4,

20-16 =4,

24 -20 = 4 and so on.....

Now, substitute the value of
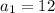`a_1 = 12` and d =4 in [1] ; we get

`a_n = a_(n-1)+4`

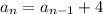
Therefore, we have;

`\left\{{{a_1=12} \atop {a_n =a_(n-1)+4}} \right`