Question

Using the graph of f(x) = log2x below, approximate the value of y in the equation 2^(2y) = 3.

Answer 1

The figure above represent the graph of
`log_(2)(x)`

We are to approximate the value of y from the equation:


`2^(2y)=3`

Taking log to the base 2 of both sides, we get:


`log_(2)(2^(2y))=log_(2)(3) \\ \\ 2y(log_(2)(2)= log_(2)(3) \\ \\ 2y=log_(2)(3) \\ \\ y= (log_(2)(3))/(2)`

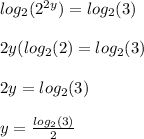
In order to find the value of y, we first need to find the value of
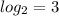
`log_(2)=3` from the graph. From the graph we can see that the value of log_{2}(3) is about 1.6, as shown in image attached with.

So,

y = 1.6/2 = 0.8

Thus value of y, as calculated using the graph is 0.8