Answer:
B.Triangles BCA and DAC are congruent according to the Angle-side-Angle (ASA) theorem.
Explanation:
We are given that ABCD is a parallelogram
AB=CD and BC= AD
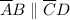 and
and
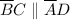
To prove that opposite sides of parallelogram ABCD are congruent.
Construct diagonal AC with a straightedge.
In triangles BCA and DAC

By reflexive property of equality

By alternate interior angles theorem
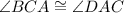
By a;ternate interior angle theorem
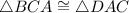
By Angle-Side-Angle (ASA) theorem
By CPCTC, opposite sides AB and CD, as well as sides BC and DA are congruent.
Hence proved.