m∠X = 54.3°.
Using the Law of Sines, we have:
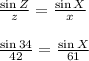
Cross multiplying gives us
61(sin 34) = 42(sin X)
Divide both sides by 42:
(61(sin 34))/42 = (42(sin X))/42
(61(sin 34))/42 = sin X
Take the inverse sine of both sides:
sin⁻¹((61(sin 34))/42) = sin⁻¹(sin X)
54.3 = X