Answer:10.67
Step-by-step explanation:The given series is a geometric series:
8 , 2 , 0.5 , ...... etc
The general formula of the geometric sequence is:
a1 , a1*r , a1*r² , ......
Comparing the general form with the given, we would find that:
a1 = 8
a1 * r = 2
Therefore:
8*r = 2
r = 2/8 = 0.25
We can double check using another term as follows:
a1 = 8
a1*r² = 0.5
8r² = 0.5
r² = 0.5/8 = 0.0625
r = √0.0625 = 0.25
Now, we will get the sum of the sequence as follows:
S =
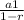
=
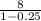
= 32/3 = 10.67
Hope this helps :)